Answer:
you have to find 4 spring with this elastic constant k = 316 N / m
Step-by-step explanation:
In this case for the design of the dispenser the four springs are placed in the four corner at the bottom, therefore we can use the translational equilibrium relationship
4 F_e -W = 0
where the elastic force is
F_e = k x
we substitute
4 kx = mg
k =
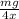
Each tray has a thickness of x = 0.450 cm = 0.450 10⁻² m, this should be the elongation of the spring so that when the tray is in position it will remain fixed.
let's calculate
k =

k = 3.1578 10² N / m
k = 316 N / m
therefore you have to find 4 spring with this elastic constant