Answer:
g ±Δg = (9.8 ± 0.2) m / s²
Step-by-step explanation:
For the calculation of the acceleration of gravity they indicate the equation of the simple pendulum to use
T =
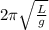
T² =
 4pi2 L / g
4pi2 L / g
g =
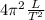
They indicate the average time of 20 measurements 1,823 s, each with an oscillation
let's calculate the magnitude
g =
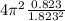 4 pi2 0.823 / 1.823 2
4 pi2 0.823 / 1.823 2
g = 9.7766 m / s²
now let's look for the uncertainty of gravity, as it was obtained from an equation we can use the following error propagation
for the period
T = t / n
ΔT =
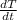 Δt +
Δt +
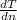 ΔDn
ΔDn
In general, the number of oscillations is small, so we can assume that there are no errors, in this case the number of oscillations of n = 1, consequently
ΔT = Δt / n
ΔT = Δt
now let's look for the uncertainty of g
Δg =
 ΔL +
ΔL +
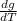 ΔT
ΔT
Δg =
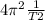 ΔL + 4π²L (-2 T⁻³) ΔT
ΔL + 4π²L (-2 T⁻³) ΔT
a more manageable way is with the relative error
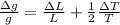
we substitute
Δg = g ( \frac{\Delta L }{L} + \frac{1}{2} \frac{\Delta T}{T}DL / L + ½ Dt / T)
the error in time give us the stanndard deviation
let's calculate
Δg = 9.7766 (
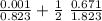 )
)
Δg = 9.7766 (0.001215 + 0.0184)
Δg = 0.19 m / s²
the absolute uncertainty must be true to a significant figure
Δg = 0.2 m / s2
therefore the correct result is
g ±Δg = (9.8 ± 0.2) m / s²