Answer:
It will take 24 minutes before they are on the same problem.
Explanation:
Caroline is on number 12 and can solve 1 math problem in 1.5 minutes.
Per minute, she solved
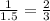 of a problem. So, after t minutes, she will be on the problem:
of a problem. So, after t minutes, she will be on the problem:
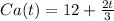
Chase is on number 16 and can solve 1 math problem in 2 minutes.
Per minute, he solved
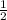 of a problem. So, after t minutes, he will be on the problem:
of a problem. So, after t minutes, he will be on the problem:
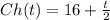
How many minutes will it take before they are on the same problem?
This is t for which:
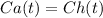
So
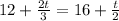
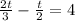
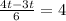
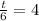
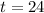
It will take 24 minutes before they are on the same problem.