Answer:
v= 20.8 m/s
Step-by-step explanation:
- Assuming no other forces acting on the ball, from the instant that is thrown vertically downward, it's only accelerated by gravity, in this same direction, with a constant value of -9.8 m/s2 (assuming the ground level as the zero reference level and the upward direction as positive).
- In order to find the final speed 2.00 s after being thrown, we can apply the definition of acceleration, rearranging terms, as follows:
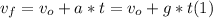
- We have the value of t, but since the ball was thrown, this means that it had an initial non-zero velocity v₀.
- Due to we know the value of the vertical displacement also, we can use the following kinematic equation in order to find the initial velocity v₀:
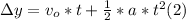
- where Δy = yf - y₀ = 15.4 m - 37.4 m = -22 m (3)
- Replacing by the values of Δy, a and t, we can solve for v₀ as follows:
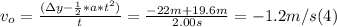
- Replacing (4) , and the values of g and t in (1) we can find the value that we are looking for, vf:
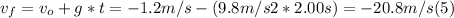
- Therefore, the speed of the ball (the magnitude of the velocity) as it passes the top of the window is 20.8 m/s.