Answer:
C.
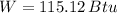
Step-by-step explanation:
Thermodynamically speaking, a Carnot engine represents an entirely reversible thermal process and its energy efficiency represents the maximum theoretical efficiency that thermal machines can reach. The efficiency of the ideal thermal process (
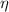 ), no unit, is:
), no unit, is:
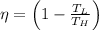 (1)
(1)
Where:
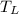 - Temperature of the cold reservoir, measured in Rankine.
- Temperature of the cold reservoir, measured in Rankine.
 - Temperature of the hot reservoir, measured in Rankine.
- Temperature of the hot reservoir, measured in Rankine.
If we know that
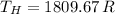 and
and
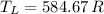 , then the energy efficiency of the ideal thermal process is:
, then the energy efficiency of the ideal thermal process is:
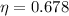
By First Law of Thermodynamics, we calculate the work output:
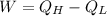
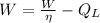 (By definition of efficiency)
(By definition of efficiency)

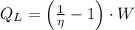 (2)
(2)
Where:
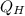 - Heat received by the engine, measured in Btu.
- Heat received by the engine, measured in Btu.
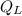 - Heat rejected by the engine, measured in Btu.
- Heat rejected by the engine, measured in Btu.
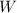 - Work output, measured in Btu.
- Work output, measured in Btu.
If we know that
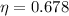 and
and
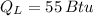 , then the work output of the Carnot engine is:
, then the work output of the Carnot engine is:
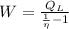
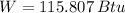
The work output of the Carnot engine is 115.807 Btu. (Answer: C)