Part (c)
We'll use this identity
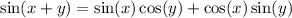
to say
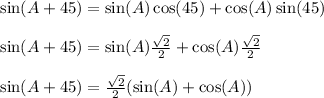
Similarly,
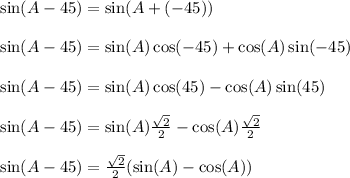
-------------------------
The key takeaways here are that
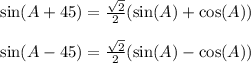
Therefore,
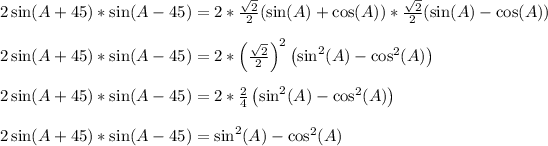
The identity is confirmed.
==========================================================
Part (d)
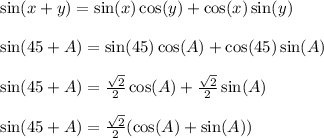
Similarly,
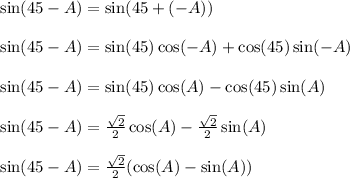
-----------------
We'll square each equation
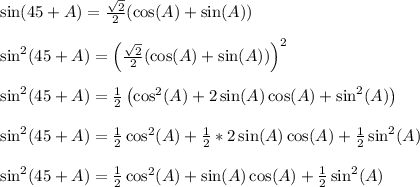
and
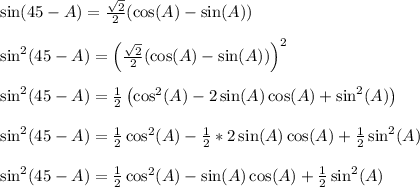
--------------------
Let's compare the results we got.
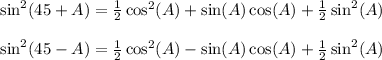
Now if we add the terms straight down, we end up with
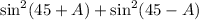 on the left side
on the left side
As for the right side, the sin(A)cos(A) terms cancel out since they add to 0.
Also note how
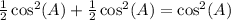 and similarly for the sin^2 terms as well.
and similarly for the sin^2 terms as well.
The right hand side becomes
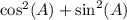 but that's always equal to 1 (pythagorean trig identity)
but that's always equal to 1 (pythagorean trig identity)
This confirms that
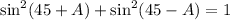 is an identity
is an identity