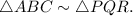Yes, triangle ABC is similar to triangle PQR
Yes, two of the three triangles are similar.
In triangle ABC, AB=5, AC=4, and BC=4.
In triangle PQR, PR=8, PQ=10, and angle RPQ=
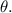
To determine if two triangles are similar, we compare the ratios of their corresponding side lengths.
Here, the ratio of AB to PQ is
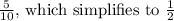 , and the ratio of AC to QR is
, and the ratio of AC to QR is
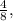 which also simplifies to
which also simplifies to
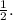
Since both ratios are equal, triangle ABC is similar to triangle PQR.
The appropriate similarity statement is: