Question

F(x)=2x^2-5x-20
find f(-9)

Answer 1

Given :-

`\sf f(x) = 2 {x}^(2) - 5x - 20`

To Find :-

`\sf f( - 9)`

Solution :-

`: \implies \sf f( - 9) = [2 *( { - 9}^(2) )]-[ 5 * - 9] - 20`

`: \implies \sf f( - 9) = 2 * 81 + 45 - 20`

`: \implies \sf f( - 9) = 162 + 45 - 20`

`: \implies \sf f( - 9) = 207 - 20`

`: \implies \bf f( - 9) = 187`

Answer 2

The output when x = -9 is f(x) = 187.

Explanation:

We are given a function and asked to find the output of that function.

• The input of a function refers to a value that is substituted into the function in order to simplify it to a final value.
• The output of a function is the value that is achieved when the input is substituted into the equation and the function is evaluated.

Our standard function is in the form of a quadratic equation.

`ax^2+bx+c=0`

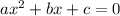
Let's check for a change in the presentation of the first value in the equation.

`\bold{f(x)} = 2x^2 - 5x - 20\\\\\bold{f(-9)}`

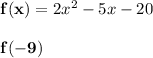
We see that x becomes -9. We also know that from conventional algebra, we need to make this change throughout the entire equation. Therefore, since we changed the x in f(x), we need to change it in 2x² - 5x - 20 as well.

`f(-9) = 2(-9)^2 - 5(-9) - 20`

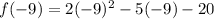
Now, it's time to simplify this function. Let's first simplify the first term of the function:
`2(-9)^2`.

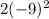Let's follow PEMDAS in order to simplify the term.

P - Parentheses

E - Exponents

M - Multiplication

D - Division

A - Addition

S - Subtraction

When using this acronym, make sure that all operations are performed left to right.

We see that -9 is raised to the power of 2, so we square -9. Otherwise, we carry out the following operation.

`-9 * -9 = 81`

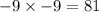
Then, we see that 2 is multiplied into this value. Therefore, we multiply 81 by 2.

`81 * 2 = 162`

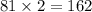
Now, we need to subtract the product of 5 and -9.

`5 * -9 = -45`

`162 - - 45 = 207`

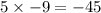
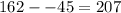
Finally, we subtract 20 from this value.

`207 - 20 = 187`

Therefore, the value of f(-9) is 187.