Answer:
See below
Explanation:
So, on the complex plane, we see that
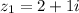
Therefore,
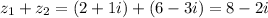
Since we added the complex numbers, we can see that the real part of
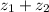 is 8 and the imaginary part of
is 8 and the imaginary part of
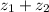 is -2. Remember that complex numbers are written in the form of
is -2. Remember that complex numbers are written in the form of
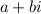 , so either the real or imaginary part can both be negative.
, so either the real or imaginary part can both be negative.