Question

The graph of an exponential function passes through (1, 10) and (4, 80). Find the function that describes the graph.

Answer 1

`y=5 \cdot 2^x`

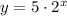
Explanation:

An exponential function is written in the form:

• 
  `y=ab^x`

We can use the given points that the exponential function passes through to solve for a and b.

Create a system of equations by substituting (1, 10) and (4, 80) into the exponential form of a function.

• 
  `\text{I}:\ 10=ab^1`
• 
  `\text{II}: \ 8 0=ab^4`

Divide Equation I by Equation II in order to cancel out variable a.

• 
  `\displaystyle (80=ab^4)/(10=ab)`
• 
  `8=b^3`
• 
  `b=2`

Now we can solve for a by substituting b back into either equation from the system of equations.

• 
  `10=ab`
• 
  `10=a(2)`
• 
  `a=5`

Substitute 5 for a and 2 for b into the form of an exponential function to find the exponential function that passes through (1, 10) and (4, 80).

• 
  `y=5 \cdot 2^x`

y = 5 · 2ˣ is the exponential function that describes the graph.

Answer 2

• y = 5*2ˣ

Explanation:

Exponential function:

• y = abˣ

Ordered pairs given:

• (1, 10) and (4, 80)

Substitute x and y values to get below system:

• 10 = ab
• 80 = ab⁴

Divide the second equation by the first one and solve for b:

• 80/10 = b³
• b³ = 8
• b = ∛8
• b = 2

Use the first equation and find the value of a:

• 10 = a*2
• a = 5

The function is:

• y = 5*2ˣ