Answer:
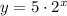
Explanation:
An exponential function is written in the form:
We can use the given points that the exponential function passes through to solve for a and b.
Create a system of equations by substituting (1, 10) and (4, 80) into the exponential form of a function.
Divide Equation I by Equation II in order to cancel out variable a.
Now we can solve for a by substituting b back into either equation from the system of equations.
Substitute 5 for a and 2 for b into the form of an exponential function to find the exponential function that passes through (1, 10) and (4, 80).
y = 5 · 2ˣ is the exponential function that describes the graph.