Question

Estimate the area

Use a Right Riemann

sum with the three sub-intervals given in the table.

Answer 1

B

Explanation:

We are given that:

`f(x)\geq g(x)`

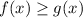
For all real numbers and they form a region R that is bounded from x = 1 to x = 7. A table of values is given.

We are directed to use a Right Riemann Sum to find the area between the curves of f and g.

Since f is greater than g for all values of x, to find the approximate area between f and g, we can first find the area of f and then subtract the area of g from f.

Using a Right Riemann Sum, the area of f is approximately:

(We multiply the width between each x-coordinate by the right endpoint)

`\displaystyle \int_1^7f(x)\, dx\approx3(5)+2(2)+1(8)=27`

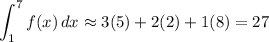
And the area of g is approximately:

`\displaystyle \int_1^7g(x)\, dx\approx3(1)+2(0)+1(5)=8`

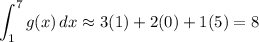
Therefore, the area between them will be:

`A=\displaystyle \int_1^7f(x)\, dx-\int_1^7 g(x)\, dx\approx 27-8=19`

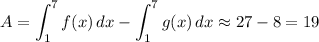
Our answer is B.