Answer:

Explanation:
A polynomial is given to us and we need to find the value of the constants in the given equation . The given polynomial to us is :-
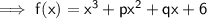
It's mentioned that (x - 1) is a factor of f(x) . This means on putting x = 1 in the given polynomial the value of the polynomial becomes 0 .
Puttting x = 1 in f(x) :-
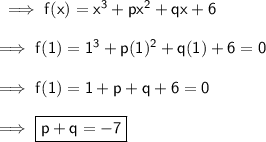

Now secondly it's given that on dividing the given polynomial by (x + 1) , the remainder is 8 . This means that on putting x = -1 the value of the given polynomial becomes 8 .
Puttting x = (-1) :-
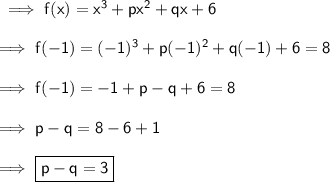

Adding the above two equations :-
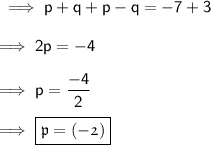

Put this value of p in equation (i) .
