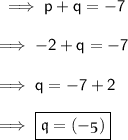Question

5. f(x) = x ^ 3 + p * x ^ 2 + qx + 6 (a) Find the value of each constants p and q, given that (x - 1) is a factor of f(x) and when f(x) is divided by (x + 1) the remainder is 8. (b) Hence, solve the equation f(x) = 0

Answer 1

`\boxed{\textsf{ The value of p is \textbf{-2} and the value of q is \textbf{ -5}.}}`

Explanation:

A polynomial is given to us and we need to find the value of the constants in the given equation . The given polynomial to us is :-

`\sf\implies f(x)= x^3+px^2+qx + 6`

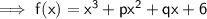
It's mentioned that (x - 1) is a factor of f(x) . This means on putting x = 1 in the given polynomial the value of the polynomial becomes 0 .

Puttting x = 1 in f(x) :-

`\sf\implies f(x)= x^3+px^2+qx + 6 \\\\\sf\implies f(1) = 1^3 + p(1)^2+q(1) + 6 = 0 \\\\\sf\implies f(1)= 1+p + q + 6 = 0 \\\\\sf\implies \boxed{ \red{\sf p + q = -7 }}`

`\rule{200}2`

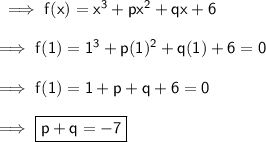
Now secondly it's given that on dividing the given polynomial by (x + 1) , the remainder is 8 . This means that on putting x = -1 the value of the given polynomial becomes 8 .

Puttting x = (-1) :-

`\sf\implies f(x)= x^3+px^2+qx + 6 \\\\\sf\implies f(-1) = (-1)^3 + p(-1)^2+q(-1)+6 = 8 \\\\\sf\implies f(-1)= -1+p -q + 6 = 8 \\\\\sf\implies p - q = 8 -6 +1 \\\\\sf\implies \boxed{ \red{\sf p - q = 3 }}`

`\rule{200}2`

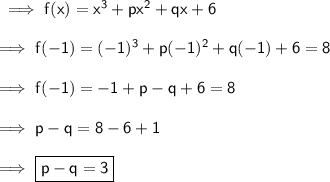
Adding the above two equations :-

`\sf\implies p + q + p - q = -7 + 3 \\\\\sf\implies 2p = -4 \\\\\sf\implies p =(-4)/(2)\\\\\sf\implies \boxed{\pink{\frak{ p = (-2) }}}`

`\rule{200}2`

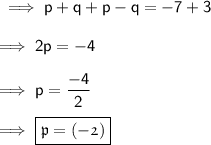
Put this value of p in equation (i) .

`\sf\implies p + q = -7 \\\\\sf\implies -2 + q = -7 \\\\\sf\implies q = -7+2 \\\\\sf\implies \boxed{\pink{\frak{ q = (-5) }}}`