Question

A teenager who is 5 feet tall throws an object into the air. The quadratic function LaTeX: f\left(x\right)=-16x^2+64x+5f ( x ) = − 16 x 2 + 64 x + 5 is where f(x) is the height of the object in feet and x is the time in seconds. When will the ball be 10 feet in the air?

Answer 1

At approximately x = 0.08 and x = 3.92.

Explanation:

The height of the ball is modeled by the function:

`f(x)=-16x^2+64x+5`

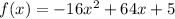
Where f(x) is the height after x seconds.

We want to determine the time(s) when the ball is 10 feet in the air.

Therefore, we will set the function equal to 10 and solve for x:

`10=-16x^2+64x+5`

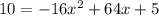
Subtracting 10 from both sides:

`-16x^2+64x-5=0`

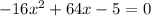
For simplicity, divide both sides by -1:

`16x^2-64x+5=0`

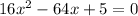
We will use the quadratic formula. In this case a = 16, b = -64, and c = 5. Therefore:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

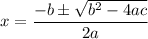
Substitute:

`\displaystyle x=(-(-64)\pm√((-64)^2-4(16)(5)))/(2(16))`

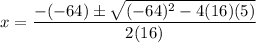
Evaluate:

`\displaystyle x=(64\pm√(3776))/(32)`

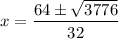
Simplify the square root:

`√(3776)=√(64\cdot 59)=8√(59)`

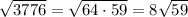
Therefore:

`\displaystyle x=(64\pm8√(59))/(32)`

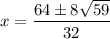
Simplify:

`\displaystyle x=(8\pm√(59))/(4)`

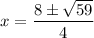
Approximate:

`\displaystyle x=(8+√(59))/(4)\approx 3.92\text{ and } x=(8-√(59))/(4)\approx0.08`

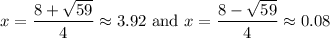
Therefore, the ball will reach a height of 10 feet at approximately x = 0.08 and x = 3.92.