Answer :
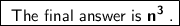
Explanation:
Its given that n is the middle out of the three consecutive integers . So ,
The last integer will be :-

The next Integer will be :-
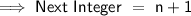
Now the Question says that the three integers are multipled to give a product . So that would be.
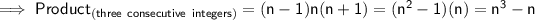
Now thirdly it's given that n is added to the given integer . That would be ,
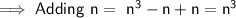
Here - n and +n gets cancelled. So we are ultimately left out with n³.
Hence the final number is a cube of some number.