Question

Let us suppose that one of the fireworks is launched from the top of the building with an initial upward velocity of 150 ft/s and the building has a height of 35 feet. what is the equation for this situation?

Answer 1

9.6 seconds

Explanation:

The equation for projectile motion in feet is
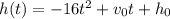`h(t)=-16t^2+v_0t+h_0` where
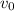`v_0` is the initial velocity in ft/s and
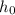`h_0` is the initial height in feet.

We are given that the initial upward velocity is
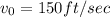`v_0=150ft/sec` and the initial height is
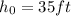`h_0=35ft`. Thus, plugging these values into our equation, we get
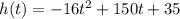`h(t)=-16t^2+150t+35` as our equation for the situation.

The firework will land, assuming it doesn't explode, when
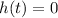`h(t)=0`, thus:

`h(t)=-16t^2+150t+35\\\\0=-16t^2+150t+35\\\\t=(-b\pm√(b^2-4ac))/(2a)\\ \\t=(-150\pm√(150^2-4(-16)(35)))/(2(-16))\\ \\t=(-150\pm√(22500+2240))/(-32)\\\\t=(-150\pm√(24740))/(-32)\\\\t=(-150\pm2√(6185))/(-32)\\ \\t=(75\pm√(6185))/(16)\\\\t_1\approx-0.2\\\\t_2\approx9.6`

Since time can't be negative, then the firework will land after 9.6 seconds, assuming it doesn't explode at the time of landing.