Question

Since the degree of the numerator is less than the degree of the denominator, we don't need to divide. We factor the denominator as

Answer 1

As given,

I =
`\int\limits {(3x)/(x^(2) - 2x) } \, dx`

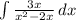
Since the degree of the numerator is less than the degree of the denominator, we don't need to divide.

We factor the denominator as x(x-2)

The partial fraction decomposition is

`(3x)/(x^(2) - 2x) = (3x)/(x(x-2)) = (A)/(x) + (B)/(x-2)\\ = (A(x-2) + B(x))/(x(x-2)) \\`

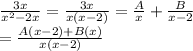
we get

3x = A(x-2) + B(x)

⇒3x = x(A+B) - 2A

By comparing , we get

A+ B = 3 , -2A = 0

⇒A = 0 and B = 3- A = 3-0 = 3

∴ we get

A = 0, B = 3

Therefore, the integral become
`\int\limits {(3x)/(x^(2) - 2x) } \, dx = \int\limits {[(0)/(x) + (3)/(x-2) ] } \, dx`