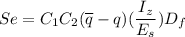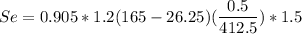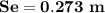Answer:
Step-by-step explanation:
From the given information:
The square foundation = 3m by 3m
capacity q = 165 kPa
depth = 1.5 m
assuming soil unit weight = 17.5 kN
q = 17.5 × 1.5
q = 26.25 kPa
Settlement
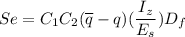
where;
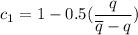

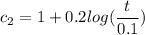
suppose t = 1year
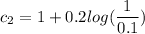

Using Schertmann method.
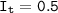
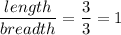
∴
E⁵ =
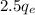
E⁵ = 2.5 × 165
E⁵ = 412.5 kPa
Hence: