Question

Calculate the acceleration due to gravity at Earth due to the Moon. (b) Calculate the acceleration due to gravity at Earth due to the Sun.

Answer 1

a) g’= 3.44 10⁻⁵ m / s²

b) g ‘’ = 5.934 10⁻³ m / s²

Step-by-step explanation:

For this exercise let's use the law of universal gravitation

F =
`G (m M)/(r^2)`

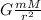
where m is the mass of the body under study, M the mass of the body that creates the force and r the distance between the bodies

F =
`m \ ( G (M)/(r^2) )`

the attractive force is called weight W = m g,

Thus

g =
`G (M)/(r^2)`

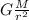
is called the acceleration of gravity

a) the acceleration created by the moon

g' = G \frac{M}{r^2}

the mass of the moon is M = 7.36 10²² kg

the distance from the moon to the Earth's surface is

r = D -R_e

r = 3.84 10⁸ -6.37 10⁶

r = 3.7763 10⁸ m

we calculate

g’=
`6.67 \ 10^(-11) \ (7.36 \ 10^(22))/( (3.7763 \ 10^8)^2)`

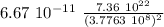
g ’= 3.44 10⁻⁵ m / s²

b) the acceleration created by the sun

mass of the sun M = 1,9991 10³⁰ ka

the distance from the sun wears down the Earth's surface

r = D -R_e

r = 1.496 10¹¹ -6.37 10⁶

r = 1.4959 10¹¹ m

let's calculate

g ’’ =
`6.67 \ 10^(-11) (1.991 \ 10^(30))/( (1.4959 \ 10^(11))^2 )`

g ‘’ = 5.934 10⁻³ m / s²