Question

Consider quadrilateral EFGH.

Quadrilateral E F G H is shown. Sides F G and E H are parallel. Angles E and H are congruent. The length of E F is 4 n minus 4, the length of F G is 3 n + 3, and the length of G H is 2 n + 6.

What is the length of line segment GH?

5 units
7 units
16 units
24 units

Answer 1

the answer is C

Explanation:

:]

Answer 2

Given:

In quadrilateral EFGH,
`FG\parallel EH,\angleE\cong \angle H,EF=4n-4,FG=3n+3, GH=2n+6`

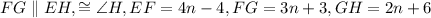
To find:

The length of segment GH.

Solution:

Draw a figure according to the given information as shown below.

In quadrilateral EFGH,
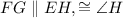`FG\parallel EH,\angleE\cong \angle H`, it means the quadrilateral EFGH is an isosceles quadrilateral because base angles are equal.

Now, quadrilateral EFGH is an isosceles quadrilateral, so the sides EF and GH are equal.

`EF=GH`

`4n-4=2n+6`

`4n-2n=4+6`

`2n=10`

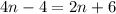
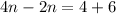
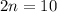
Divide both sides by 2.

`n=(10)/(2)`

`n=5`

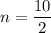
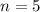
Now,

`GH=2n+6`

`GH=2(5)+6`

`GH=10+6`

`GH=16`

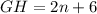
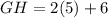
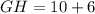
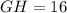
Therefore, the correct option is C.