Answer:
327.58 kPa
Step-by-step explanation:
Given data; 1st wave
Amplitude ( A1 ) = 293 Kpa
frequency = 6Hz
Average stress = 2388kPa
phase angle = 90° ( leading )
Determine the amplitude of the second sinusoidal component in kPa
Amplitude of additional wave ( A2 ) = 293 / 2 = 146.5 kPa
Amplitude of first wave ( A 1 ) = 293 kPa
hence the amplitude of the second sinusoidal component
A' =
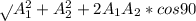
=
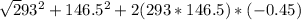
=
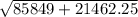
= 327.58 kPa