Question

Decide whether ABCD with vertices A (3,8) B (6,5) C (5,4) , and D (2,7) is a rectangle a rhombus or a square

Answer 1

Given:

The vertices of the quadrilateral ABCD are A(3,8), B(6,5), C(5,4), and D(2,7).

To find:

Whether the given quadrilateral is a rectangle, a rhombus or a square.

Solution:

Distance formula: The distance between two points is

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

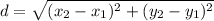
Using distance formula, the side lengths are:

`AB=√(\left(6-3\right)^2+\left(5-8\right)^2)`

`AB=√(\left(3\right)^2+\left(-3\right)^2)`

`AB=√(9+9)`

`AB=√(18)`

`AB=3√(2)`

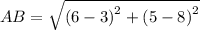
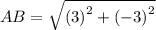
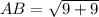
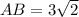
Similarly,

`BC=√(\left(5-6\right)^2+\left(4-5\right)^2)=√(2)`

`CD=√(\left(2-5\right)^2+\left(7-4\right)^2)=3√(2)`

`AD=√(\left(2-3\right)^2+\left(7-8\right)^2)=√(2)`

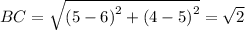
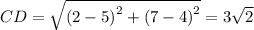
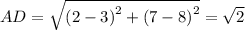
The length of diagonals are:

`AC=√(\left(5-3\right)^2+\left(4-8\right)^2)=2√(5)`

`BD=√(\left(2-6\right)^2+\left(7-5\right)^2)=2√(5)`

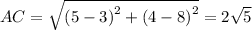
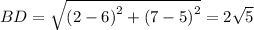
From the above calculation, we conclude that the given quadrilateral has two pairs of congruent opposite sides and equal diagonals.

Opposite sides of a rectangle are equal and its diagonals are also equal.

Therefore, the given quadrilateral ABCD is a rectangle.