Question

For all functions of the form f(x) = ax2 + bx + c, which is true when b = 0?

The graph will always have zero x-intercepts.
The function will always have a minimum.
The y-intercept will always be the vertex.
The axis of symmetry will always be positive.

Answer 1

The y-intercept will always be the vertex.

Explanation:

its c

Answer 2

C) The y-intercept will always be the vertex.

Explanation:

We have the quadratic function in the form:

`f(x)=ax^2+bx+c`

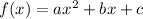
And we want to determine the true statement when b = 0.

Let's go through each of the choices and examine its validity.

Choice A)

Recall that according to the quadratic formula, the roots of a function is given by:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

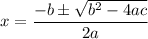
If b = 0, then we acquire:

`\displaystyle x=(-(0)\pm√((0)^2-4ac))/(2a)=\pm(√(-4ac))/(2a)`

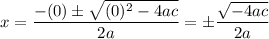
As we can see, as long as the inside of the square root is positive, the graph will have x-intercepts. So, b equalling zero does not guarantee that the graph does not have any x-intercepts.

A is false.

Choice B)

A quadratic has a minimum if it curves upwards and a maximum if it curves downwards.

This is decided by the leading coefficient a. b does not affect whether a quadratic curves downwards or upwards.

B is false.

Choice C)

The vertex of a quadratic is given by:

`\displaystyle \text{Vertex}=\left(-(b)/(2a), f\left(-(b)/(2a)\right)\right)`

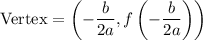
If b = 0, then the x-coordinate of the vertex is given by:

`\displaystyle x=-((0))/(2a)=0`

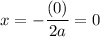
Then the y-coordinate will be:

`f(0)=a(0)^2+b(0)+c=c`

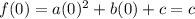
So, the vertex is (0, c).

This is also the y-intercept as, by definition, the y-intercept is the value when x = 0.

So, Choice C is the correct choice.

Choice D)

The axis of symmetry is the x-coordinate of the vertex. As we saw earlier, the x-coordinate of the vertex will always be:

`\displaystyle x=-((0))/(2(a))=0`

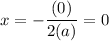
Zero is neither positive nor negative. Thus, D is false.