Answer:
C) The y-intercept will always be the vertex.
Explanation:
We have the quadratic function in the form:

And we want to determine the true statement when b = 0.
Let's go through each of the choices and examine its validity.
Choice A)
Recall that according to the quadratic formula, the roots of a function is given by:

If b = 0, then we acquire:
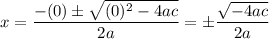
As we can see, as long as the inside of the square root is positive, the graph will have x-intercepts. So, b equalling zero does not guarantee that the graph does not have any x-intercepts.
A is false.
Choice B)
A quadratic has a minimum if it curves upwards and a maximum if it curves downwards.
This is decided by the leading coefficient a. b does not affect whether a quadratic curves downwards or upwards.
B is false.
Choice C)
The vertex of a quadratic is given by:
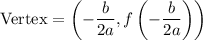
If b = 0, then the x-coordinate of the vertex is given by:
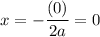
Then the y-coordinate will be:
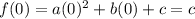
So, the vertex is (0, c).
This is also the y-intercept as, by definition, the y-intercept is the value when x = 0.
So, Choice C is the correct choice.
Choice D)
The axis of symmetry is the x-coordinate of the vertex. As we saw earlier, the x-coordinate of the vertex will always be:
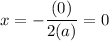
Zero is neither positive nor negative. Thus, D is false.