Answer:
The length of the AR is
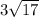 or
or
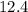 units.
units.
Explanation:
Given the endpoints of a line segment AR
We can calculate the length of AR using the formula
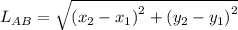
In our case,
Substituting (x₁, y₁) = (8, -2) and (x₂, y₂) = (-4, 1) in the formula
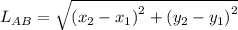
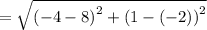
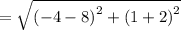 ∵ Apply rule:
∵ Apply rule:

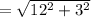
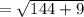
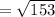
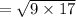
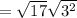 Apply radical rule:
Apply radical rule:
![\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}](https://img.qammunity.org/2022/formulas/mathematics/high-school/rehzjf30t6schvnsdsp34bb8ydt44prnxt.png)
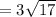 Apply radical rule:
Apply radical rule:
![\sqrt[n]{a^n}=a](https://img.qammunity.org/2022/formulas/mathematics/high-school/mq133hacm1iecdy7intzah77gs4fgjtv08.png)

Therefore, the length of the AR is
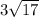 or
or
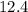 units.
units.