To find two complex numbers with a product of 20, we can start by expressing the complex numbers in the form
 , where
, where
 and
and
 are real numbers and
are real numbers and
 is the imaginary unit with the property that
is the imaginary unit with the property that
 .
.
Let's choose two complex numbers such that their product is 20. One straightforward way is to consider one complex number as
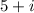 and another as
and another as
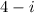 . Now, let's verify their product:
. Now, let's verify their product:
![\[ (5 + i)(4 - i) = 20 - 5i + 4i - i^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wlifwo0hywyqc7r5h1icu7fs3eyxab87ms.png)
Since
 , we have:
, we have:
![\[ (5 + i)(4 - i) = 20 - i + 4 \cdot (-1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/glt7ecnfvr4qbwipw8vuyy7jzb5p8mmrkf.png)
![\[ = 20 - i - 4 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/by0oxn5a5ucgk0drsfwaizmeeuri74nf1p.png)
![\[ = 16 - i \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3w4dxcfecyhstzzogek0hc25qhsgxo9pmr.png)
However, this product is not 20, so we need to adjust our numbers. Let's use the fact that
 to our advantage. We can choose two complex numbers such that the real part of their product is 20 and the imaginary parts cancel out.
to our advantage. We can choose two complex numbers such that the real part of their product is 20 and the imaginary parts cancel out.
One simple pair would be
 and
and
 . Let's calculate their product:
. Let's calculate their product:
![\[ (2√(5) + i)(2√(5) - i) = (2√(5))^2 - (i)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x9z91d3e4i6eh8ee5y9cg8fu5cz1k2a4if.png)
![\[ = 4 \cdot 5 - (-1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4flq8alq4lhg26h2blp83pbilrts6epbxt.png)
![\[ = 20 + 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ef6sonl4d3ruqlmwc3eucecuqiunrcqbs8.png)
![\[ = 21 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mu12fz3zd2ckm0dts9yzx5pck8zdrjt24y.png)
Close, but we want exactly 20, not 21. To get exactly 20, we need two complex numbers whose real parts multiply to 20 and whose imaginary parts multiply to zero. Let's use
 (which is
(which is
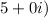 and
and
 (which is
(which is
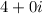 ), or any such real numbers that multiply to 20. Real numbers are a subset of complex numbers, so this is a valid choice. However, if we want non-real complex numbers, we might consider
), or any such real numbers that multiply to 20. Real numbers are a subset of complex numbers, so this is a valid choice. However, if we want non-real complex numbers, we might consider
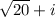 and
and
 :
:
\[ (\sqrt{20} + i)(\sqrt{20} - i) = 20 - i^2 \]
\[ = 20 + 1 \]
\[ = 21 \]
Again, this gives us 21. We seem to be stuck with an extra \( +1 \) from the \( -i^2 \) term. To get exactly 20, we need our imaginary parts, when multiplied together, to give us \( -1 \). This would mean choosing two imaginary parts that are inverses of each other, like \( i \) and \( -i \), but we must also ensure the real parts multiply to 20. Let's consider
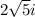 and
and
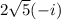 :
:
![\[ (2√(5)i)(2√(5)(-i)) = (2√(5))(2√(5))(i)(-i) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ddkrsfenem2jtygh8zj9396bgxqadc0u0w.png)
![\[ = 4 \cdot 5 \cdot (-i^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xnsczxx126ew9mj4bmkjl80j0aic59siu4.png)
![\[ = 20 \cdot 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7a1m3ty5h724ceh7k3r6o870xapolvc70z.png)
![\[ = 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/392mic3bniu9ne055u9xf5b5fwwi39mw20.png)
So, two complex numbers with a product of 20 are
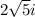 and
and
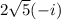 .
.
Now, regarding how complex numbers are related to quadratic equations:
Complex numbers are deeply connected to quadratic equations because they allow us to find solutions to quadratics even when no real solutions exist. When the discriminant of a quadratic equation (the part under the square root in the quadratic formula \( b^2 - 4ac \)) is negative, there are no real roots because you cannot take the square root of a negative number in the set of real numbers. However, with complex numbers, you can take the square root of a negative number by introducing the imaginary unit \( i \).
For example, the quadratic equation
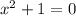 has no real solutions because there's no real number whose square is -1. But in the complex number system, it has two solutions:
has no real solutions because there's no real number whose square is -1. But in the complex number system, it has two solutions:
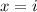 and
and
 . Thus, complex numbers extend the real number system to ensure that every quadratic equation has a solution, which is known as the Fundamental Theorem of Algebra.
. Thus, complex numbers extend the real number system to ensure that every quadratic equation has a solution, which is known as the Fundamental Theorem of Algebra.