Show that there is a number d such thatlim x2 + 2dx − d + 6x→3 x2 − 3x \\exists, and plug-in your value d to compute the limit.

Question

`Show that there is a number d such thatlim x2 + 2dx − d + 6x→3 x2 − 3x \\exists, and plug-in your value d to compute the limit.`

Answer 1

• d = -3
• limit = 0

Explanation:

You want the value of d such that the limit exists, and you want to know what that limit is in ...

`\displaystyle\lim_(x\to3)(x^2+2dx-d+6)/(x^2-3x)`

Limit exists

The denominator has zeros at x=0 and x=3. If the zero at x=3 is not canceled by a numerator zero there, then the rational function will change signs between x=3+ and x=3-. When that happens, the limit will not exist.

To cancel the denominator zero at x=3, we must choose a value of d that makes the numerator zero there:

At x=3, the numerator becomes ...

3² +2·3·d -d +6 = 15 +5d

We want that to be zero, so we have ...

5(d +3) = 0

d = -3 . . . . . . . the value of d so the limit exists

Limit

Then the limit is ...

`\displaystyle\lim_(x\to3)(x^2-6x+9)/(x^2-3x)=\lim_(x\to3)((x-3)^2)/(x(x-3))=\lim_(x\to3)(x-3)/(x) = (3-3)/(3)=0`

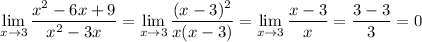
The limit as x → 3 is zero (0).

<95141404393>