The value of x is 86.
To find the value of x in the given rectangle
 , we need to use the fact that the opposite angles in a rectangle are congruent.
, we need to use the fact that the opposite angles in a rectangle are congruent.
Since
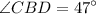 , we know that
, we know that
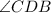 is also
is also
 . Similarly, since
. Similarly, since
 is a rectangle, we have
is a rectangle, we have
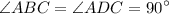 .
.
Now, let's focus on triangle
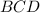 . The sum of the angles in a triangle is always
. The sum of the angles in a triangle is always
 . So, we can write an equation based on the angles in triangle
. So, we can write an equation based on the angles in triangle
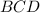 :
:
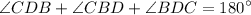
Substituting the given values:
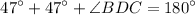
Simplifying:
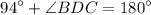
Subtracting
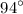 from both sides:
from both sides:
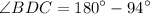
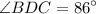
Since
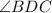 is an angle in a triangle, it must be less than
is an angle in a triangle, it must be less than
 . Therefore,
. Therefore,
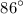 is a valid value for
is a valid value for
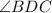 .
.