Question

A 20 g ball of clay is thrown horizontally at 30 m/s toward a 1.0 kg ball sitting at rest on a frictionless surface. The clay hits and sticks to the block.

a. What impulse does the clay exert on the block?

b. What impulse does the block exert on the clay?

c. Does
`J_(block.on.clay) = -J_(clay.on.block)`?

Answer 1

a. The clay exerts an impulse of 600 N·s on the block.

b. The block exerts an impulse of -600 N·s on the clay.

Step-by-step explanation:

Understanding impulse and its conservation is crucial in analyzing this scenario. Impulse is the product of force and time, and it's equal to the change in momentum. In this case, the clay hitting and sticking to the block alters their momenta.

a. The impulse exerted by the clay on the block is equal to the change in momentum of the block. The clay's initial momentum is calculated as the product of its mass (20 g) and velocity (30 m/s). As the clay sticks to the block, their combined mass is used to find the final velocity. The change in momentum is then calculated, yielding an impulse of 600 N·s.

b. The block, initially at rest, experiences a change in momentum as it gains the momentum of the clay. The impulse exerted by the block on the clay is equal in magnitude but opposite in direction to that of the clay. Using the principle of conservation of momentum, the block's final velocity is calculated, resulting in an impulse of -600 N·s.

In summary, the impulses are equal in magnitude due to the conservation of momentum, but they differ in direction, representing the action and reaction between the clay and the block.

Answer 2

The results of the calculations:

a. The impulse exerted on the block by the clay is
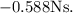`\(-0.588 \text{Ns}\).`This is the change in momentum of the clay, which is the mass of the clay multiplied by the change in its velocity
`(which is \( v_{\text{final}} - v_{\text{clay,initial}} \)).`

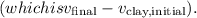
b. The impulse exerted on the clay by the block is \(0.588 \text{Ns}\). It's equal in magnitude but opposite in direction to the impulse exerted by the clay on the block, as per Newton's third law.

c. Since the impulses are equal in magnitude and opposite in direction, this confirms that
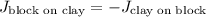`\( J_{\text{block on clay}} = -J_{\text{clay on block}} \)`is indeed true, which is consistent with Newton's third law of motion.

The final velocity of both the clay and the block sticking together after the collision is approximately
`\(0.588 \text{m/s}\).`

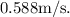
To solve the physics problem presented, we'll go through it step by step. The situation described is a perfectly inelastic collision where a ball of clay hits and sticks to another ball.

Given:

- Mass of clay ball,
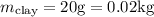`\( m_{\text{clay}} = 20 \text{g} = 0.02 \text{kg} \)`(converted from grams to kilograms)

- Velocity of clay ball before collision,
`\( v_{\text{clay,initial}} = 30 \text{m/s} \)`

- Mass of the block, \( m_{\text{block}} = 1.0 \text{kg} \)

- Velocity of the block before collision
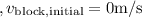`, \( v_{\text{block,initial}} = 0 \text{m/s} \)` (since it's at rest)

After the collision, the clay and block stick together and move as a single object.

a. The impulse exerted on the block by the clay is given by the change in momentum of the clay ball:

`\[ J = \Delta p = m_{\text{clay}} \cdot (v_{\text{final}} - v_{\text{clay,initial}}) \]`

We don't yet know \( v_{\text{final}} \), the final velocity of the combined mass after the collision, but we can find it using the conservation of momentum, since no external forces are acting on the system:

`\[ m_{\text{clay}} \cdot v_{\text{clay,initial}} + m_{\text{block}} \cdot v_{\text{block,initial}} = (m_{\text{clay}} + m_{\text{block}}) \cdot v_{\text{final}} \]`

b. By Newton's third law, the impulse that the block exerts on the clay is equal in magnitude and opposite in direction to the impulse the clay exerts on the block:

`\[ J_{\text{block on clay}} = -J_{\text{clay on block}} \]`

c. Therefore
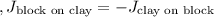`, \( J_{\text{block on clay}} = -J_{\text{clay on block}} \)` is true by the principle of Newton's third law.