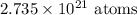Answer: 2.735 x 10²¹
Step-by-step explanation:
Given:
Atomic mass of tin
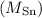 = 118.71 g/mol
= 118.71 g/mol
Percent of Sn present = 5.80%
Mass of Sn
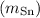 = 93.0 g
= 93.0 g
To calculate moles:
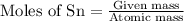

One mole
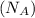 contains Avogadro's number
contains Avogadro's number
 of atoms.
of atoms.
Therefore, 0.23 moles of Sn contains:

The total number of atoms in naturally occurring Sn can be calculated using the percentage of the heaviest isotope:
Percentage of heaviest isotope of tin (
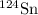 ) = 5.80%
) = 5.80%
Total number of atoms in tin (
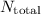 ) =
) =

Total number of atoms of (
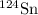 ) in naturally occurring tin (
) in naturally occurring tin (
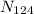 ) is therefore =
) is therefore =