Question

Given is a resistor R=10kΩ. There is a current of IR=4mA across the resistor. Which power rating is needed for this resistor? a) 0.25 W b) 0.5 W c) 0.125 W d) 1 W

Answer 1

To calculate the necessary power rating for the resistor, square the current (converted to amperes), multiply by the resistance, and then choose the rating that safely exceeds the calculated power dissipation.

Step-by-step explanation:

To determine the power rating needed for a resistor with resistance R=10kΩ and a current of IR=4mA flowing through it, we apply the power formula P = I2R. First, we convert the current from milliamperes to amperes by dividing by 1000, which gives us 0.004 A. Then, we square the current and multiply by the resistance:

P = (0.004 A)2 × 10,000 Ω = 0.000016 × 10,000 = 0.16 W.

Since 0.16 W is closest to the option (b) 0.5 W, this would be the safest power rating to ensure the resistor can handle the dissipation without overheating.

Answer 2

The power rating needed for this resistor is 0.25

Correct answer (a)

To determine the power rating needed for the resistor, we can use the formula that relates power (P) to current (I) and resistance (R):

`\[ P = I^2 * R \]`

where

- P is the power in watts (W),

- I is the current in amperes (A),

- R is the resistance in ohms (Ω).

Given:

- R = 10,000 Ω (since 1 kΩ = 1,000 Ω)

- \
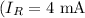`( I_R = 4 \) mA` = 0.004 A (since 1 mA = 0.001 A)

Let's calculate the power ( P ):

P = (0.004
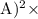`\text{ A})^2 *`10,000 Ω}

P = (0.000016
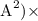`\text{ A}^2) *` 10,000 Ω

`\[ P = 0.16 \text{ W} \]`

Now let's determine which of the given options is the correct power rating for the resistor. The actual power dissipated is 0.16 W. The resistor should have a power rating that is equal to or greater than this value to ensure safe operation. We'll round up to the next highest standard value.

Looking at the options, 0.16 W is less than 0.25 W, so the correct power rating needed for the resistor would be:

a) 0.25 W

This choice would provide a sufficient safety margin for the resistor's operation.