Question

Helpppppppppppppppppppppppppppp

Answer 1

(6, 5)

Explanation:

The orthocenter of a triangle is the point of intersection of all three altitudes (perpendicular lines drawn from each vertex to the opposite side). For an acute angle triangle, the orthocenter lies inside the triangle.

To find the orthocenter of the given triangle DEF, we need to find the equations of two altitudes. To do this, begin by finding the slopes of two sides of the triangle. Calculate the negative reciprocal of these slopes to find the slopes of the altitudes. Finally, use the point-slope formula with the vertex contained by each altitude to determine their equations.

Altitude from vertex D

`\textsf{Slope\;of\;$\overline{EF}$}=(y_F-y_E)/(x_F-x_E)=(1-3)/(8-2)=(-2)/(6)=-(1)/(3)`

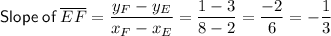
As the slope of the altitude is the negative reciprocal, the slope of the altitude is m = 3.

Substitute m = 3 and point D(6, 5) into the point-slope formula to find the equation of the altitude:

`\begin{aligned}y-y_1&=m(x-x_1)\\y-5&=3(x-6)\\y-5&=3x-18\\y&=3x-13\end{aligned}`

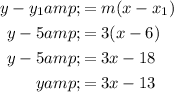
Altitude from vertex E

`\textsf{Slope\;of\;$\overline{DF}$}=(y_F-y_D)/(x_F-x_D)=(1-5)/(8-6)=(-4)/(2)=-2`

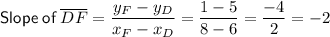
As the slope of the altitude is the negative reciprocal, the slope of the altitude is m = 1/2.

Substitute m = 1/2 and point E(2, 3) into the point-slope formula to find the equation of the altitude:

`\begin{aligned}y-y_1&=m(x-x_1)\\\\y-3&=(1)/(2)(x-2)\\\\y-3&=(1)/(2)x-1\\\\y&=(1)/(2)x+2\end{aligned}`

Orthocenter

To find the x-coordinate of the orthocenter, substitute the first altitude equation into the second altitude question and solve for x:

`\begin{aligned}3x-13&=(1)/(2)x+2\\\\(5)/(2)x&=15\\\\5x&=30\\\\x&=6\end{aligned}`

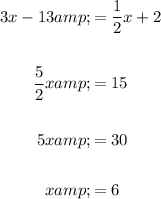
Substitute the found value of x into one of the altitude equations and solve for y:

`y=3(6)-13=5`

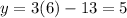
Therefore, the coordinates of the orthocenter are (6, 5).

• The orthocenter is vertex D.
• The triangle is a right triangle, where ∠D = 90°.
• The triangle is an isosceles triangle, where DE = DF.