Question

PLEASE HELP ASAP TYSM​

Answer 1

• 5. 5
• 6. 5.1
• 7. 8

Task :

• To find the measure of x in each of the given triangles.

Solution :

We know that,

• If two angles and one side is given,we can find the measure of the other side using the law of sines.

Law of sines is given by :

• 
  `(a)/( \sin(a) ) = (b)/( \sin(b) ) \\`

wherein,

• a & b = The sides of the triangle
• sin(a) & sin (b) = the angles opposite to the respective sides.

5.

In the given triangle,

• a = 5
• sin a = 180° - (90° + 45°) = 45°
• b = x
• sin b = 45°

Plugging in the values,

• 
  `(5)/( \sin(45) ) = (x)/( \sin(45) ) \\`
• 
  `(5)/( 0.71) = (x)/( 0.71 ) \\`
• 
  `x= (5 * 0.71)/(0.71) \\`
• 
  `x = 5`

Thus, the value of x would be equal to 5 units.

6.

In the given triangle,

• a = x
• sin (a) = 23°
• b = 13
• sin (b) = 90°

Plugging in the values,

• 
  `(x)/( \sin(23) ) = (13)/( \sin(90) ) \\`
• 
  `(x)/( 0.39 ) = (13)/( 1 ) \\`
• 
  `x = 13 * 0.39`
• 
  `x = 5.07`
• 
  `x = 5.1`

Thus, the value of x would be equal to 5.1 units.

7.

In the given triangle,

• a = 16
• sin (a) = 90°
• b = x
• sin (b) = 180° - (90° + 60°) = 30°

Plugging in the values,

• 
  `(16)/( \sin(90) ) = (x)/( \sin(30) ) \\`
• 
  `(16)/(1) = (x)/(0.5) \\`
• 
  `x = 16 * 0.5`
• 
  `x = 8`

Thus, the value of x would be equal to 8 units.

Answer 2

5) x = 5

6) x = 5.1

7) x = 8

Explanation:

To find the values of x in the given right triangles, we can use the trigonometric ratios:

`\boxed{\begin{array}{l}\underline{\sf Trigonometric\;ratios}\\\\\sf \sin(\theta)=(O)/(H)\qquad\cos(\theta)=(A)/(H)\qquad\tan(\theta)=(O)/(A)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{O is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{A is the side adjacent the angle.}\\\phantom{ww}\bullet\;\textsf{H is the hypotenuse (the side opposite the right angle).}\\\\\end{array}}`

`\hrulefill`

Question 5

From observation of the given right triangle:

• θ = 45°
• O = x
• A = 5

As we have been given the lengths of the sides opposite and adjacent angle A, we can use the tangent ratio to find the value of x:

`\tan \theta=\sf (O)/(A)`

`\tan 45^(\circ)=(x)/(5)`

`5\tan 45^(\circ)=x`

`x=5\tan 45^(\circ)`

`x=5 \cdot 1`

`x=5`

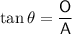
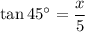
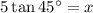
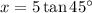
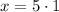
Therefore, the value of x is 5.

`\hrulefill`

Question 6

From observation of the given right triangle:

• θ = 23°
• O = x
• H = 13

As we have been given the hypotenuse and the length of the side opposite angle B, we can use the sine ratio to find the value of x:

`\sin \theta=\sf (O)/(H)`

`\sin 23^(\circ)=(x)/(13)`

`13\sin 23^(\circ)=x`

`x=13 \sin 23^(\circ)`

`x=5.07950467...`

`x=5.1\; \sf (nearest\;tenth)`

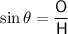
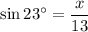
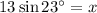
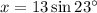
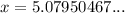
Therefore, the value of x is 5.1 (rounded to the nearest tenth).

`\hrulefill`

Question 7

From observation of the given right triangle:

• θ = 60°
• A = x
• H = 16

As we have been given the hypotenuse and the length of the side adjacent angle A, we can use the cosine ratio to find the value of x:

`\cos \theta=\sf (A)/(H)`

`\cos 60^(\circ)=(x)/(16)`

`16 \cos 60^(\circ)=x`

`x=16 \cos 60^(\circ)`

`x=16 \cdot (1)/(2)`

`x=8`

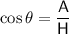
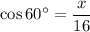
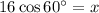
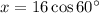
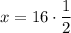
Therefore, the value of x is 8.