Question

What is the sum of the series sum from n equals 1 to infinity of negative 4 times five eighths to the n power question mark

Answer 1

`S_(\infty)=-(20)/(3)`

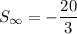
Explanation:

Given sigma notation:

`\displaystyle \sum_(n=1)^(\infty) -4\left((5)/(8)\right)^n`

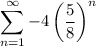
As the formula for the terms is in the form
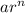`ar^n`, the series is geometric.

Find the first and second terms, by substituting n = 1 and n = 2 into the formula for the terms:

`a_1= -4\left((5)/(8)\right)^1=-(5)/(2)`

`a_2= -4\left((5)/(8)\right)^2=-(25)/(16)`

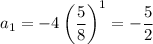
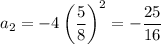
Find the common ratio (r) by dividing the second term by the first term:

`r=(a_2)/(a_1)=(-(25)/(16))/(-(5)/(2))=(5)/(8)`

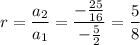
To find the sum of an infinite geometric series, we can use the formula:

`\boxed{\begin{array}{l}\underline{\textsf{Sum of an infinite geometric series}}\\\\S_(\infty)=(a)/(1-r),\;\;\textsf{for}\;|r| < 1\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$a$ is the first term.}\\ \phantom{ww}\bullet\;\textsf{$r$ is the common ratio.}\end{array}}`

In this case, the value of r is 5/8. Since |5/8| < 1, the sum exists.

Substitute a = -5/2 and r = 5/8 into the formula for the sum of an infinite geometric series:

`S_(\infty)=(-(5)/(2))/(1-(5)/(8))`

`S_(\infty)=(-(5)/(2))/((3)/(8))`

`S_(\infty)=-(5)/(2)\cdot (8)/(3)`

`S_(\infty)=-(40)/(6)`

`S_(\infty)=-(20)/(3)`

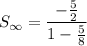
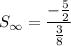
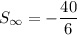
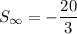
Therefore, the sum of the given series is:

`\Large\boxed{\boxed{-(20)/(3)}}`