Question

100 points image below

Answer 1

θ = 12.4° (1 d.p.)

Explanation:

The given diagram shows a right triangle, where the hypotenuse is the length of a zip wire, measuring 65 m. The height of this triangle is the difference between the starting height of the zip wire (26 m) and its ending height (12 m), resulting in a vertical height of 14 m.

To find the size of angle θ, we can use the sine trigonometric ratio:

`\boxed{\begin{array}{l}\underline{\textsf{Sine trigonometric ratio}}\\\\\sf \sin(\theta)=(O)/(H)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{O is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{H is the hypotenuse (the side opposite the right angle).}\end{array}}`

In this case:

• O = 14 m
• H = 65 m

Substitute the values of O and H into the sine ratio and solve for angle θ:

`\sin(\theta)=(14)/(65)`

`\theta=\sin^(-1)\left((14)/(65)\right)`

`\theta=12.438092815...^(\circ)`

`\theta=12.4^(\circ)\; \sf (1\;d.p.)`

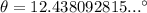
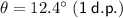
Therefore, the size of angle θ is 12.4°, rounded to one decimal place.