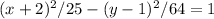Final answer:
To find the equation of the hyperbola, use the standard form of the equation and substitute the given values of the vertices and foci. Equation comes to be
Step-by-step explanation:
To find the equation of a hyperbola given the vertices and foci, we can use the standard form of the equation:
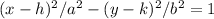
where (h, k) is the center of the hyperbola, and a and b represent the distance from the center to the vertices and from the center to the foci, respectively.
Given that the vertices are (-2, -4) and (-2, 6), we can determine that the center is (-2, 1) since it lies in the horizontal midline between the vertices. Moreover, the distance from the center to the vertices is 5, so a will be equal to 5. The distance from the center to the foci is 8, so b will be equal to 8.
Using these values, we can substitute into the standard form equation and get: