Question

$40,500 are deposited into an account with a 3.8% interest rate, compounded monthly.

Find the accumulated amount after 20 years. Round to the nearest cent (hundredth).

Answer 1

$86,496.26.

Explanation:

Definition of compound interest:

Compound interest is interest that is calculated on the principal amount plus any accrued interest. This means that the interest is earned on both the initial deposit and the interest that has already been earned.

To calculate the accumulated amount after 20 years, we can use the following formula:

`\sf A = P\left(1 + (r)/(n)\right)^(nt)`

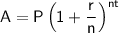
where:

• A is the accumulated amount
• P is the principal amount (initial deposit)
• r is the interest rate (as a percentage)
• n is the number of times the interest is compounded per year
• t is the number of years

In this case, we have:

• P = $40,500
• r = 3.8% (divided by 100 to get a decimal) =0.038
• n = 12 (since the interest is compounded monthly)
• t = 20

Substituting these values into the formula, we get:

`\sf A = 40,500\left(1 + (0.0382)/(12)\right)^(12* 20)`

`\sf A = 40,500(1.003167)^(240)`

`\sf A = 86,496.26`

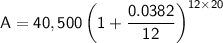
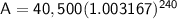
Therefore, the accumulated amount after 20 years is $86,496.26.

Answer 2

$86,496.26

Explanation:

To find the account balance after 20 years of $40,500 deposited into an account with an interest rate of 3.8% compounded monthly, we can use the compound interest formula.

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Given values:

• P = $40,500
• r = 3.8% = 0.038
• n = 12 (monthly)
• t = 20 years

Substitute the given values into the formula and solve for A:

`A=40500\left(1+(0.038)/(12)\right)^(12 * 20)`

`A=40500\left(1.0031666666...\right)^(240)`

`A=40500\left(12.13571012...\right)`

`A=86496.259924...`

`A=86496.26\; \sf (nearest\;hundredth)`

Therefore, the account balance after 20 years is $86,496.26 (rounded to the nearest cent).