Question

Find the area of the blue shaded region in the figure, assuming the quadrilateral inside the circle is a square.

Answer 1

`\textsf{Shaded Area}=36\pi-72 \approx 41.4\; \sf square\;units`

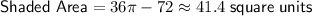
Explanation:

To find the area of the blue shaded region, we need to subtract the area of the inscribed square from the area of the circle.

The equation of a circle is given by (x - h)² + (y - k)² = r², where (h, k) represents the center of the circle, and r is its radius.

In the case of the circle x² + y² = 36, we can see that the center is at the origin (0, 0) and its radius is 6 units.

The equation for the area of a circle with radius r is A = πr².

Therefore, the area of the given circle is:

`\begin{aligned}\textsf{Area$_(\sf circle)$}&=\pi \cdot 6^2\\&=36\pi\; \sf square\;units\end{aligned}`

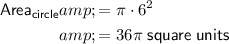
From observation of the given diagram, we notice that the four corners of the square touch the circumference of the circle. Therefore, the diagonal of the square is equal to the diameter of the circle. Since the diameter of a circle is twice its radius, and in this case the radius of the circle is 6 units, the diagonal of the square is 12 units.

To find the area of the square, we first need to determine its side length (s). To do this, we can use the Pythagorean Theorem, where the hypotenuse is the diagonal of the square, and the legs are the side lengths:

`\begin{aligned}s^2+s^2&=12^2\\2s^2&=144\\s^2&=72\\s&=√(72)\\s&=√(36 \cdot 2)\\s&=√(36) √(2)\\s&=6√(2)\end{aligned}`

Now that we have the side length of the square, we can find its area by squaring its side length. Therefore, the area of the square is:

`\begin{aligned}\textsf{Area$_(\sf square)$}&=\left(6√(2)\right)^2\\&=72\; \sf square\;units\end{aligned}`

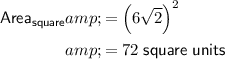
To find the area of the blue shaded region, subtract the area of the inscribed square from the area of the circle:

`\begin{aligned}\sf Area_(\sf shaded\;region)&=\sf Area_(\sf circle)-Area_(\sf square)\\&=36\pi - 72\\&=113.0973355...-72\\&=41.0973355...\\&=41.1\; \sf square\;units\;(nearest\;tenth)\end{aligned}`

Therefore, the area of the blue shaded region is exactly (36π - 72) square units, which is approximately 41.1 square units (rounded to the nearest tenth).