The magnitude of charge
 on each sphere, with a potential difference of
on each sphere, with a potential difference of
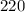 volts, is approximately
volts, is approximately
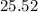 nanoCoulombs (nC).
nanoCoulombs (nC).
To solve this problem, let's break it down into the two parts you've outlined:
Part (a): Finding the Radius of the Outer Sphere
Step 1: Understand the Formula for Capacitance of a Spherical Capacitor
The capacitance
 of a spherical capacitor with an inner radius
of a spherical capacitor with an inner radius
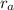 and an outer radius
and an outer radius
 in a vacuum is given by:
in a vacuum is given by:
![\[ C = 4\pi \varepsilon_0 (r_a r_b)/(r_b - r_a) \]](https://img.qammunity.org/2024/formulas/physics/high-school/5eybeezrgytwekfy060zpbkus5c2qee9l7.png)
Step 2: Plug in Known Values and Solve for

Given:
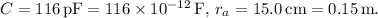
Rearrange the formula to solve for
 :
:
![\[ r_b = (C)/(4\pi \varepsilon_0 r_a) + r_a \]](https://img.qammunity.org/2024/formulas/physics/high-school/kcigwgmvh7z65xpohhd44vuokavm8vouef.png)
Part (b): Finding the Magnitude of Charge on Each Sphere
Step 1: Understand the Relationship Between Capacitance, Voltage, and Charge
The capacitance
 s related to the potential difference
s related to the potential difference
 and the charge
and the charge
 by:
by:
![\[ C = (Q)/(V) \]](https://img.qammunity.org/2024/formulas/physics/college/ihmikp31kugvwuhwznss5i099m2m9l0mwy.png)
Rearrange to solve for
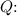
![\[ Q = C \cdot V \]](https://img.qammunity.org/2024/formulas/physics/high-school/dfba5vgc1f3gut8yr0et8560glxnc2m7mb.png)
Step 2: Plug in Known Values to Find

Given:
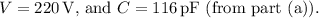
Calculate
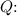
![\[ Q = 116 * 10^(-12) \, \text{F} * 220 \, \text{V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/yk1ids7b2yqdx4itly30ke7sory69hpy44.png)
Let's perform these calculations.
Solution
Part (a): Radius of the Outer Sphere
The radius of the outer sphere
 is approximately
is approximately
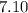 meters.
meters.
Part (b): Magnitude of Charge on Each Sphere
The magnitude of charge
 on each sphere, with a potential difference of
on each sphere, with a potential difference of
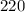 volts, is approximately
volts, is approximately
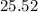 nanoCoulombs (nC).
nanoCoulombs (nC).