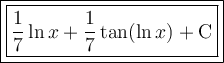Question

Evaluate the following integral. Please show steps. (IMAGE BELOW)

Answer 1

`(1)/(7)\ln x+(1)/(7)\tan (\ln x) +\text{C}`

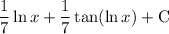
Explanation:

Given indefinite integral:

`\displaystyle \int (1+\sec^2(\ln x))/(7x)\; \text{d}x`

To integrate the given integral, we can use the method of substitution.

`\textsf{Let}\;\;u=\ln x`

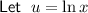
Differentiate u with respect to x:

`\frac{\text{d}u}{\text{d}x}=(1)/(x)`

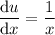
Rearrange to isolate dx:

`\text{d}x=x\;\text{d}u`

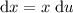
Rewrite the original integral in terms of u and du:

`\begin{aligned}\displaystyle \int (1+\sec^2(\ln x))/(7x)\; \text{d}x&=\int (1+\sec^2(u))/(7x)\cdot x\;\text{d}u\\\\&=\int (1+\sec^2(u))/(7)\;\text{d}u\end{aligned}`

Take out the constant 1/7:

`\displaystyle=(1)/(7)\int 1+\sec^2(u)\;\text{d}u`

We can now evaluate the integral by using the following integration rules:

`\boxed{\begin{minipage}{5.1 cm}\underline{Integrating a constant}\\\\$\displaystyle \int n\:\text{d}x=nx+\text{C}$\\\\(where $n$ is any constant value) \end{minipage}}`

`\boxed{\begin{minipage}{5.1 cm}\underline{Integrating $\sec^2 kx$}\\\\$\displaystyle \int \sec^2 kx\:\text{d}x=(1)/(k) \tan kx\:\:(+\text{C})$\end{minipage}}`

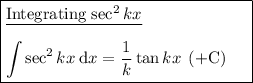
Therefore:

`\begin{aligned}\displaystyle (1)/(7)\int 1+\sec^2(u)\;\text{d}u&=(1)/(7)\left[u+\tan u]+\text{C}\\\\&=(1)/(7)u+(1)/(7)\tan u +\text{C}\end{aligned}`

Substitute back u = ln x:

`=(1)/(7)\ln x+(1)/(7)\tan (\ln x) +\text{C}`

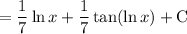
Therefore, the evaluation of the given integral is:

`\large\boxed{\boxed{(1)/(7)\ln x+(1)/(7)\tan (\ln x) +\text{C}}}`