Question

Given the functions below, find f(g(x))

Answer 1

• Option (3) 4x² - 34x + 72

Given :

• f(x) = x² - x
• g(x) = 9 - 2x

To find :

• f(g(x))

Solution :

We are given that,

• f(x) = x² - x ....(1)

Also ,

• g(x) = 9-2x....(2)

Substituting the value of g(x) in the function given,

• f(g(x)) = (9-2x)² - (9-2x)
• f(g(x)) = 4x² - 36x + 81 - 9 + 2x
• f(g(x)) = 4x² - 36x + 2x + 72
• f(g(x)) = 4x² - 34x + 72

Thus, option (3) 4x² - 34x + 72 is correct ✓.

`\\`

Answer 2

`\textsf{C)} \quad 4x^2-34x+72`

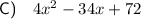
Explanation:

A composite function is a mathematical operation that combines two (or more) functions by applying one function's output as the input for another function to create a new function.

Given functions:

`f(x)=x^2-x`

`g(x)=9-2x`

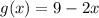
To determine the composite function f(g(x)), substitute the output of function g(x) as the input of function f(x). In other words, replace the x-variable of function f(x) with function g(x).

`\begin{aligned}f(g(x))&=f(9-2x)\\&=(9-2x)^2-(9-2x)\\&=(9-2x)(9-2x)-9+2x\\&=81-36x+4x^2-9+2x\\&=4x^2+2x-36x+81-9\\&=4x^2-34x+72\end{aligned}`

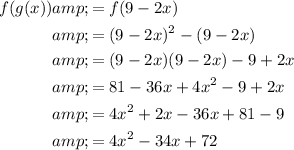
Therefore, the composite function f(g(x)) is:

`\Large\boxed{\boxed{f(g(x))=4x^2-34x+72}}`