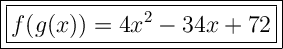Answer:
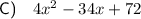
Explanation:
A composite function is a mathematical operation that combines two (or more) functions by applying one function's output as the input for another function to create a new function.
Given functions:
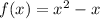
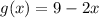
To determine the composite function f(g(x)), substitute the output of function g(x) as the input of function f(x). In other words, replace the x-variable of function f(x) with function g(x).
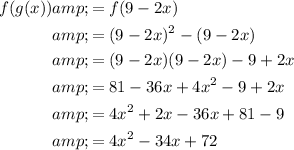
Therefore, the composite function f(g(x)) is: