Question

A company sells widgets. The amount of profit, y, made by the company, is related to the selling price of each widget, x, by the given equation. Using this equation, find out the maximum amount of profit the company can make, to the nearest dollar. y=-29x^2+1388x-10040

Answer 1

Given:

The amount of profit, y, made by the company, is related to the selling price of each widget, x, by the given equation

`y=-29x^2+1388x-10040`

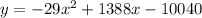
To find:

The maximum amount of profit the company can make, to the nearest dollar.

Solution:

If a quadratic equation is
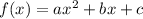`f(x)=ax^2+bx+c`, then the vertex is

`Vertex=\left(-(b)/(2a),f(-(b)/(2a))\right)`

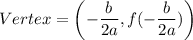
If a>0, then vertex is the minimum point and if a<0, then the vertex is the maximum point.

We have,

`y=-29x^2+1388x-10040`

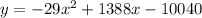
Here,
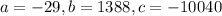`a=-29,b=1388, c=-10040`. Clearly, a<0. So, the vertex is the point of maxima.

`-(b)/(2a)=-(1388)/(2(-29))`

`-(b)/(2a)=-(1388)/(-58)`

`-(b)/(2a)\approx 23.931`

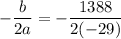
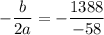
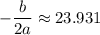
Putting x=23.931 in the given equation, we get

`y=-29(23.931)^2+1388(23.931)-10040`

`y=-16608.09+33216.228-10040`

`y=6568.138`

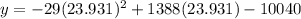
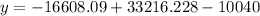
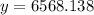
The vertex is at (23.931,6568.138).

Therefore, the maximum profit is $6568.138 when x=23.931.