Given:
The amount of profit, y, made by the company, is related to the selling price of each widget, x, by the given equation
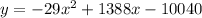
To find:
The maximum amount of profit the company can make, to the nearest dollar.
Solution:
If a quadratic equation is
 , then the vertex is
, then the vertex is
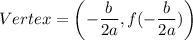
If a>0, then vertex is the minimum point and if a<0, then the vertex is the maximum point.
We have,
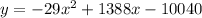
Here,
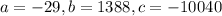 . Clearly, a<0. So, the vertex is the point of maxima.
. Clearly, a<0. So, the vertex is the point of maxima.
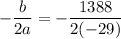
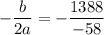
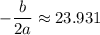
Putting x=23.931 in the given equation, we get
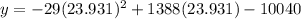
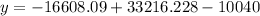
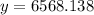
The vertex is at (23.931,6568.138).
Therefore, the maximum profit is $6568.138 when x=23.931.