2 Answers

Pjanssen · Answer 1 · 2024-09-08T01:10:25+0000

Slope

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

Let's solve the problem given to us today! The problem is the following:

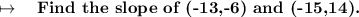
$\mapsto\quad\textbf{Find the slope of (-13,-6) and (-15,14).}$

We need to find the slope of the line passing through these two points.

__________________________________________________________

Use the slope formula to find the slope.

__________________________________________________________

The slope formula is,

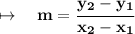
$\mapsto\quad\bf{m=\cfrac{y_2-y_1}{x_2-x_1}}$

Substitute the values:

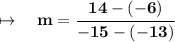
$\mapsto\quad\bf{m=\cfrac{14-(-6)}{-15-(-13)}}$

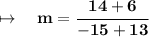
$\mapsto\quad\bf{m=\cfrac{14+6}{-15+13}}$

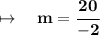
$\mapsto\quad\bf{m=\cfrac{20}{-2}}$

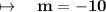
$\mapsto\quad\bf{m=-10}$

Therefore, the slope is -10.

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

Sean Taylor · Answer 2 · 2024-09-11T14:42:30+0000

Answer:

slope = - 10

Explanation:

calculate the slope m using the slope formula

m =
(y_(2)-y_(1) )/(x_(2)-x_(1) )

let (x₁, y₁ ) = (- 13, - 6 ) and (x₂, y₂ ) = (- 15, 14 )

substitute these values into the formula for m

m =
(14-(-6))/(-15-(-13)) =
(14+6)/(-15+13) =
(20)/(-2) = - 10