Question

Find the slope of the line that goes through the points (-13,-6) and (-15,14).​

Answer 1

Slope

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

Let's solve the problem given to us today! The problem is the following:

`\mapsto\quad\textbf{Find the slope of (-13,-6) and (-15,14).}`

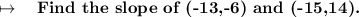
We need to find the slope of the line passing through these two points.

__________________________________________________________

Use the slope formula to find the slope.

__________________________________________________________

The slope formula is,

`\mapsto\quad\bf{m=\cfrac{y_2-y_1}{x_2-x_1}}`

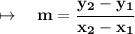
Substitute the values:

`\mapsto\quad\bf{m=\cfrac{14-(-6)}{-15-(-13)}}`

`\mapsto\quad\bf{m=\cfrac{14+6}{-15+13}}`

`\mapsto\quad\bf{m=\cfrac{20}{-2}}`

`\mapsto\quad\bf{m=-10}`

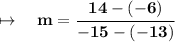
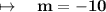
Therefore, the slope is -10.

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

Answer 2

slope = - 10

Explanation:

calculate the slope m using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

let (x₁, y₁ ) = (- 13, - 6 ) and (x₂, y₂ ) = (- 15, 14 )

substitute these values into the formula for m

m =
`(14-(-6))/(-15-(-13))` =
`(14+6)/(-15+13)` =
`(20)/(-2)` = - 10