Question

Find the general solution of the given differential equation. y^(8) +8y ^(4) +16y=0

Answer 1

The general solution to the given differential equation is
`$y= \pm 2 i$`.

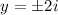Substitution:

Define
`$z=y^4$`.

Substitute z into the equation, resulting in
`$z^2+8 z+16=0$`

Factoring the Quadratic:

Factor the quadratic as
`$(z+4)(z+4)=0$`

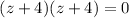
Therefore,
`$z=-4$`

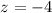
Back-Substitution:

Substitute z back into
`$z=y^4$`, yielding
`$y^4=-4$`

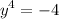
Finding Roots:

Take the fourth root of both sides, but consider complex roots:

`$y= \pm \sqrt[4]{-4}=\pm \sqrt[4]{4} \cdot \sqrt[4]{-1} y= \pm 2 \cdot( \pm i)= \pm 2 i, \pm 2 i$`

Therefore, the general solution to the differential equation is
`$y= \pm 2 i$`.

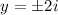Key Point:

• The original equation involves
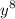  `$y^8$`, indicating the possibility of complex roots.
• Taking the fourth root of a negative number introduces imaginary units (
  `i`).
• The general solution involves complex numbers, not real numbers.