Question

Graphing inequality's

Answer 1

`\boxed{\textsf {The red area is the required answer . }}`

Explanation:

A linear inequality in two variables is given to us and we need to plot it's graph .So the the given inequality is ,

`\sf\implies y \geq- (1)/(5)x +5`

So firstly let's simplify out the inequality for easy plotting of the graph .

`\sf\implies y \geq- (1)/(5)x +5 \\\\\sf\implies y \geq (-x+5(-5))/(5)\\\\\sf\implies y \geq (-x-25)/(5)\\\\\sf\implies y \geq -(1)(x+25)/(5)`

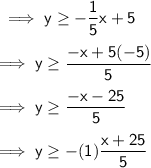
Now let's put some values of x to get values of y .

• Firstly put x = 0 then we get , y is greater than or equal to 0+5/5 (-1) = 5/5(-1) = -1 . Hence we get y ≥ (-1) .

• Secondly put x = 1 , then we get , y is greater than or equal to 1+5/5(-1)=6/5(-1) = -6/5 . Hence we get y ≥ -6/5 .

• Thirdly put x = -1 , then we get y is greater than or equal to -1+5/5(-1) = -4/5 . Hence we get y ≥ -4/5

• Fourthly put x = (-5) , then we get y is greater than or equal to -5+5/5(-1) = 0 .Hence we get y ≥ 0 .

With reference to these let's plot a graph . For the graph kindly refer to the attachment :) .

Here in the graph the red area shows the possible values of x and y .