Question

F(x)= x^3 +3

G(x)= x^2 +2
Approximate the solution to the equation f(x) = g(x) using three iterations of successive approximation. Use this graph as a starting point.

Answer 1

`x = ( - 13)/(16)`

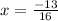
Explanation:

`f(x) = {x}^(3) + 3 \\ g(x) = {x}^(2) + 2`

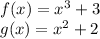
At the point of intersection, f(x)=g(x)

`{x}^(3) + 3 = {x}^(2) + 2 \\ collect \: like \: terms \\ {x}^(3) - {x}^(2) + 3 - 2 = 0 \\ {x}^(3) - {x}^(2) + 1 = 0`

`{x}^(3) - {x}^(2) + 1 = 0`

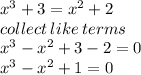
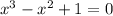
The above graph is that of the equation

`{x}^(3) - {x}^(2) + 1 = 0`

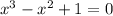
The solution is = -0.755 which is approximately -0.8

From the option provided;

For option A, x = -13/16 = -0.8125

For option B, x = -5/4 = -1.25

For option C, x = -15/16 = -0.9375

For option D, x = -7/8 = -0.875

From the option provided, The closest to the solution is Option A

Because - 0.8125 is approximately -0.8